Rational Roots Test: Worked Examples
Purplemath
When using the Rational Roots Test, always keep in mind that the Test spits out *possible* zeroes. The Test's results might not contain *any* of the actual roots of a polynomial. And remember that the Test only works on polynomials with integer coefficients. If your polynomial has, say, a square root or π as a coefficient, then don't bother with the Test.
And when you're asked to "find all possible" rational roots, keep in mind that you're just finding a list; you're not doing any solving or factoring or graphing. Yet.
- Find all possible rational x-intercepts of y = 2x3 + 3x − 5.
Keeping in mind that x-intercepts are zeroes, I will use the Rational Roots Test.
The constant term of this polynomial is 5, with factors 1 and 5.
The leading coefficient is 2, with factors 1 and 2.
Then the Rational Roots Tests yields the following possible solutions:
Whatever you do, don't forget the "plus-or-minus" on the solution. You either need to list out all the possible solutions separately, as I did in previous example; or use a "plus-or-minus" in front of each possible solution, as I showed here; or put one "plus-or-minus" in front of the whole list of possible solutions, as I will show in the next example. Just make sure you have a "plus-or-minus" in there somewhere.
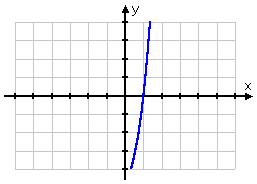
By the way, as the graph below shows, if there does turn out to be a rational root for y = 2x3 + 3x − 5, it has to be at x = 1.
- Use the Rational Roots Test to find all possible rational zeroes of 6x4 − 11x3 + 8x2 − 33x − 30.
This problem will be more complicated than the previous one, because the leading coefficient is not a simple "1".
The constant term is 30, with factors 1, 2, 3, 5, 6, 10, 15, and 30.
The leading coefficient is 6, with factors 1, 2, 3, and 6.
Then the Rational Roots Test yields:
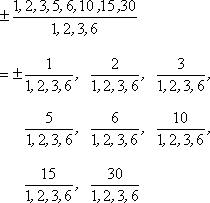
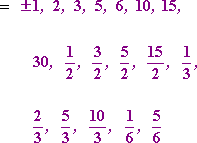
Yes, this is a very long list. You should *expect* at least some of your homework exercises and at least one test question to be as long as this.
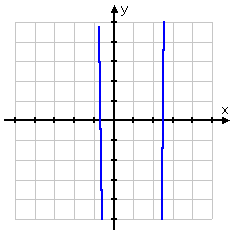
Check out the graph of the polynomial from this exercise:
You can see from the graph that there may be rational roots at and , but it would probably not make sense to try any of the other listed potential zeroes.
In those last two examples, please note how I was orderly in listing out the fractions, taking the time to reduce each fraction and to discard duplicates from the list. Take the time to work in the same orderly fashion, because this really is a simple topic, and it would be a shame if you lost easy points on the test due to carelessness.
© 2024 Purplemath, Inc. All right reserved. Web Design by 