Geometry Word Problems:
    The Box Problem & The Goat Problem (page 5 of 6)

Sections: Introduction, Basic examples, Triangle formulas, Complex examples, The Box Problem & the Goat Problem, Max / Min problems

The following are a couple of "classic" types of exercises. Almost all students eventuall see one or both of these, in some form.

• You need to make a pizza box. You know that the box needs to be two inches deep, it needs to be a square, and the web site you found said that the box needs to have a volume of 512 cubic inches. After cursing the occasional near-uselessness of the information you find on the Internet, you start calculating the dimensions you will need.

You have a large piece of cardboard, but you don't have enough cardboard to make a mistake and try again, so you'll have to get it right the first time. You will be forming the box by cutting out a large square, and then cutting out the two-inch squares from the corners that will allow you to fold up the edges to make a two-inch-deep box. What should be the dimensions of the large square? (Ignore the top of the box:  you'll just make another open box, slightly larger, turn it upside down, and slip it over the first box to make the "top".)

Visually, this is what I'm doing:

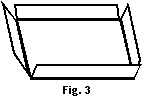
	This square stands for my initial piece of cardboard, out of which I'll be cutting corner squares and folding up the sides. The square's dimensions are x inches by x inches, but I don't know the value of x yet.
	Now I have cut the corners out, leaving two-inch flaps on all four sides. I will be folding the sides up along those red lines.
	Now I have folded up the flaps to make a two-inch deep box. (I will be taping the corners to hold them together.)

I will use "x" to stand for both the length and the width of the original square of cardboard in the computations that follow. The value of x is what I'm looking for.

Looking at the picture, I can see that the width of the bottom of my box will be x – 2 – 2; that is, the final width of the box will be the sheet's original x inches, minus two inches on either side because of the portions that I'll be losing to the flaps I'll be folding up. Then the width of the bottom of my box is going to be x – 4. By the same reasoning, the length will also be x – 4.

Since the depth of my box is 2 (that's the whole point of the two-inch-by-two-inch squares that I'm cutting out of the corners), I can write the formula for the volume of this box as:

volume = (length)(width)(depth) = 512 cubic inches
(x – 4)(x – 4)(2) = 512
2(x² – 8x + 16) = 512
x² – 8x + 16 = 256
x² – 8x – 240 = 0
(x – 20)(x + 12) = 0
x = 20  or  x = –12

I can ignore the extraneous negative result. Then x = 20 inches, and the answer is:

The large piece of cardboard should be twenty inches square.

Warning: "Twenty inches square" is not the same as "twenty square inches". "Twenty inches square" means "twenty inches on a side", for a total area of four hundred square inches. "Twenty square inches" is just that: twenty square inches.     Copyright © Elizabeth Stapel 2000-2011 All Rights Reserved

• A goat is tied to the corner of a 5-by-4-meter shed by a 8-meter piece of rope. Rounded to the nearest square meter, what is the area grazed by the goat?

What formula could they be expecting me to use for this? How on earth would I answer this? When in doubt, it can be helpful to draw a picture, so let's see what I can find:

The goat is tied at the upper right-hand corner with the dot. Now what? Well, on the nearest two sides, the goat can go this far:

This is three-quarters of a circle with radius 8 (the full length of the rope). The goat can walk around the far corners as far as the rope will allow. Along the top side, five meters of rope will be stretched along the side, leaving another three meters "in play"; along the right-hand side, four meters will have been used, leaving another four meters:

These new areas are both quarter-circles, one with radius 3 and the other with radius 4. And there will be no way for the goat to reach the opposite corner or "overlap" in grazing, because he's out of rope. So these three partial circles mark off the total grazing area.

I know the formula for the area of a circle. To find, say, the area of 3/4 of a circle, I'd just multiply the total area by 3/4. So the total area is:

(3/4)(pi)(8²) + (1/4)(pi)(3²) + (1/4)(pi)(4²)
     = 48pi + 2.25pi + 4pi = 54.25pi

I'm supposed to give my answer in terms of the nearest whole unit, so I'll plug the above into my calculator, and round:

The goat can graze about 170 square meters of grass.

Note how drawing the picture allowed me to "see" what I needed to do, immediately simplying my work. If you have "no idea" what to do, try drawing a picture. (There is an extension of this exercise, which has the goat's areas overlapping at that opposite corner. The exact solution involves trigonometry or calculus.)

<< Previous  Top  |  1 | 2 | 3 | 4 | 5 | 6  |  Return to Index  Next >>

  Copyright © 2000-2012  Elizabeth Stapel   |   About   |   Terms of Use

Contact Us