Inverses of Trigonometric Ratios
Purplemath
You've learned how to use trig ratios to solve right triangles, finding the lengths of the sides of triangles.
But what if you have the side lengths, and you need to find the triangle's angle measures?
You know that you can take side lengths and find trig ratios, and you know you can find trig ratios (in your calculator) for angles. What is missing is a way to go from the ratios back to the original angles. And that is what inverse trig values are all about.
What are inverse trigonometric ratios?
Inverse trigonometric ratios are inverse functions for sine, cosine, and tangent. While you plug angle measures into sine, cosine, and tangent to find side lengths, you plug side lengths into inverse sine, inverse cosine, and inverse tangent to find angle measures.
Can my calculator do inverse trig ratios?
Any calculator that can work with sines, cosines, and tangents will also be able to work with their inverses, usually as a second function of the regular trig buttons.
If you look at your calculator, you should see, right above the sin, cos, tan buttons, notations along the lines of sin−1, cos−1, and tan−1, or possibly asin, acos, and atan. These are what you'll be using to find angles from ratios.
What does the a in asin, acos, and atan stand for?
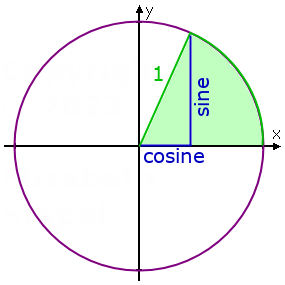
The a in asin, acos, and atan stands for "arc"; in this context, the arc is the portion of the circumference of the unit circle that corresponds to the angle measure in question. In other words, in a geometrical sense, the arc-functions tell you the angle that matches a length that is a portion of the unit circle's circumference. As Wikipedia puts it, "in the unit circle, 'the arc whose cosine is x' is the same as 'the angle whose cosine is x', because the length of the arc of the circle in radii is the same as the measurement of the angle in radians."
...which is a long way of stating what the above graphic displays; namely, that the sine and cosine of the right triangle inside the unit-circle's (green-shaded) sector are given by the lengths of the two legs of that right triangle. So, given the length of one or another of its sides, one can find the measure of the sector's angle. And we find those measures by applying inverse trigonometric functions.
(Note: There are arc-functions and inverse trig functions for the other three trig functions — secant, cosecant, and cotangent — but I've never seen them used.)
Arc-functions undo trig functions (that is, arc-functions are inverse functions) so, for instance, atan indicates the inverse tangent function, tan−1().
The first set of notations, with the "minus one" exponent, lists the inverse sine, the inverse cosine, and the inverse tangent. The second set of notations, with the a before each name, lists the arc-sine, the arc-cosine, and the arc-tangent. These are two notations for exactly the same thing.
On inverse trig functions, what does the minus-one power mean?
Inverse trigonometric functions are, in particular, inverse functions. The minus-one power indicates an inverse function, not a reciprocal. For instance, sin−1() is the inverse of the sine function; the reciprocal of the sine function is the cosecant function, csc(). The cosecant and the inverse sine are not the same thing.
How to use your calculator to confirm how inverse trig functions work
You can see how these inverse-trig functions work: Go grab your calculator, and take the sine of some angle value between zero and ninety degrees. Whatever result you get, do the inverse sine (that is, use the sin−1 button) or the arc-sine (that is, use the asin button) of that value, and you should get the value you started with.
That's what the inverses of trig ratios do: they give you the angle that goes with that right-triangle's trig ratio.
- For the triangle below, find the measure m of angle α, to the nearest degree.
They've given me the length of the side that is opposite the angle α, and they have given me the length of the hypotenuse. From "opposite" and "hypotenuse", I can form the sine ratio:
Plugging 0.9 into sin−1 in my calculator, I get:
α = 64.15806724...
Checking the exercise text, I am reminded that there is a unit of degrees that I need to account for, along with rounding the numerical result to the nearest whole numbers. So my answer is:
m(α) = 64°
Note: There are other units for measuring angles. I'll just be using degrees here, but you may also need to use radians. If so, you'll need to set your calculator's units appropriately. If you are in degree mode, you'll get degree values, not radians, and vice versa. Make sure you're set up correctly.
- Find the measure, in degrees, of angle β, accurate to one decimal place.
They've given me the lengths of the side opposite β (being 8) and the side adjacent to β (being 9).
Since the tangent is opposite over adjacent, I can form the tangent ratio with what they've given me:
I won't use the decimal for 8/9, because that could introduce round-off error. Instead, I'll work with the exact fraction and plug tan−1 into my calculator directly. The result is β = 41.63353934....
Rounding to one decimal place and remembering to affix units to my answer, I get:
m(β) = 41.6°
- Find the length of side p and the measure of angle m, as shown on the diagram. Give each answer correct to the nearest whole number or degree.
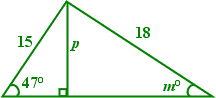
How on earth am I supposed to find the angle-measure m and the length of side p when I only have one number for that triangle? All I have is the hypotenuse! Oh, wait...
I can use the angle and hypotenuse on the left-hand triangle to find the height p for both triangles, and this will give me two numbers for the right-hand triangle. With that, I can find the measure m.
The left-hand triangle has opposite, hypotenuse, and angle, so I'll work with the sine ratio:
p = 15×sin(47°) = 10.97030552...
Now that I know that p = 11 (rounded to the nearest whole number), I can find the measure of angle m:
I'm supposed to round this angle measure to the nearest whole degree, so my answer is:
p = 11
m° = 38°
- A 5 meter ladder is leaning against a building, with the base of the ladder being two meters from the side of the building. What angle does the ladder form with the ground? Round your answer to one decimal place.
As usual, I start with a picture. It doesn't need to be "exact" or "to scale"; I just need enough of a picture to be able to keep track of what I'm doing.
With respect to the angle they want me to find (which I've indicated in the drawing above by the arc drawn in the lower left-hand vertex), I have the adjacent side and the hypotenuse, so I'll use the cosine ratio.
This is my measure, in degrees, of the angle that the bottom of the ladder makes with the ground on which it is standing. Remembering to round my answer to one decimal place, and to affix the appropriate units, my answer is that the ladder and the ground form an angle of about:
66.4°
Any time you have two sides of a triangle and need an angle, figure out the trig ratio that uses those two sides, and use the appropriate inverse button on your calculator to find the angle that goes with that ratio. And remember to put the "degree" sign on your answer any time that those are the specified units.
© 2024 Purplemath, Inc. All right reserved. Web Design by 