Solving Rational Inequalities
Purplemath
Solving rational inequalities is very similar to solving polynomial inequalities.
But because rational expressions have denominators (and therefore may have places where they're not defined), you have to be a little more careful in finding your solutions.
Content Continues Below
How do you solve rational inequalities?
To solve a rational inequality, use these steps:
Affiliate
Advertisement
- If needed, move all the terms to one side of the inequality symbol, with zero on the other side.
- If needed, combine all rational expressions into one polynomial fraction.
- Factor the numerator and denominator completely.
- Solve the factors for their zeroes; keep in mind that the denominator's zeroes would cause division by zero, so they cannot be included in your solution.
- Use the zeroes to divide the number line into intervals.
- Make a table of factors, showing where each factor is less than and greater than zero.
- Multiply the factors' signs on each interval (that is, down the table's columns) to find the sign of the rational expression on that interval.
- Select the intervals that match the inequality they gave you; remember to discard any endpoints that would cause division by zero.
Let's see how these instructions work in practice:
- Solve the following:
They've already put this inequality into (one rational expression) with (zero) on the other side. So I can start with factoring everything:
This polynomial fraction will be zero wherever the numerator is zero, so I'll set the numerator equal to zero and solve:
(x + 2)(x + 1) = 0
x + 2 = 0 or x + 1 = 0
x = −2 or x = −1
The fraction will be undefined wherever the denominator is zero, so I'll set the denominator equal to zero and solve:
(x + 4)(x − 4) = 0
x + 4 = 0 or x − 4 = 0
x = −4 or x = 4
These four values, −4, −2, −1, and +4, divide the number line into five intervals, namely:
Affiliate
(−∞, −4)
(−4, −2)
(−2, −1)
(−1, 4)
(4, +∞)
I could use "test points" to find the solution to the inequality, by picking an x-value in each interval, plugging it into the original rational expression, simplifying to get a numerical answer, and then checking the sign, but that process gets long and annoying (and is prone to errors), so I'll use the easier and faster factor-table method instead.
My factor table looks like this:
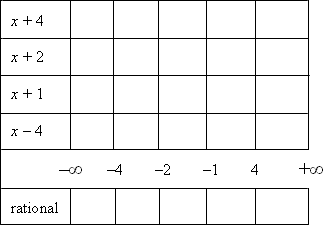
My table has one row for each factor, a row for the number line, and a row for the rational expression. Each row is split into columns, with each column corresponding to one of the intervals on the number line.
Content Continues Below
The sign of the overall rational expression is a result of the signs of its various factors, so I need to find where each factor is positive:
x + 4 > 0 for x > −4
x + 2 > 0 for x > −2
x + 1 > 0 for x > −1
x − 4 > 0 for x > 4
Now I can put "plus" signs on the intervals in each row where that row's factor is positive:

Wherever a factor isn't positive, it's negative, so I'll put "minus" signs in the remaining entries of each row:

I know that the product of an even number of "minus" signs is a plus; the product of an odd number of "minus" signs is a minus. So, by multiplying the signs down the columns (or just counting up the minusses), I get the overall sign of the rational expression on each interval:

Then the rational is positive on the intervals (−∞, −4), (−2, −1), and (4, +∞).
Looking back at the original exercise, this is an "or equal to" inequality, so I need to consider the interval endpoints, too.
If this were a polynomial inequality, I could just throw all the interval endpoints into the solution, and I'd be done. For rational expressions, though, I have to be careful not to include any x-values that would cause division by zero.
The intervals' endpoints are −4, −2, −1, and 4. I can include −2 and −1 in the solution, because they just make the expression equal to zero by making the numerator zero. But plugging −4 or 4 into the rational expression would cause division by zero, making the rational expression undefined, so I can't include these values in the solution.
Then my full solution is:
I wrote my solution above in "interval" notation. If you have to write your solution in "inequality" notation, it would look like this:
x < −4, −2 ≤ x ≤ −1, and x > 4
Don't forget: "Infinity" is not a "number" in the way that, say, "2" is. "Infinity" cannot be "included" in your solution, so never draw a square bracket next to an "infinity" "endpoint".
URL: https://www.purplemath.com/modules/ineqrtnl.htm
You can use the Mathway widget below to practice solving rational inequalities. Try the entered exercise, or type in your own exercise. Then click the button and select "Solve the Inequality for x" (or just "Solve for x") to compare your answer to Mathway's. (Or skip the widget,and continue with the lesson.
Please accept "preferences" cookies in order to enable this widget.
(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()




