Worked Examples of Solving Polynomial Inequalities
Purplemath
At this stage in your studies, you will be expected to be able to factor polynomials down to linear and quadratic factors.
For this topic, you won't be expected to find complex-valued zeroes from quadratics that don't cross the x-axis; but it will be wise to remember that these irreducible factors are either always positive or else always negative.
Content Continues Below
On the other hand, you will need to be able to solve every linear factor.
- Find the solution: (x − 5)2(x − 1)(x + 3) ≤ 0
Affiliate
For this polynomial inequality, I'm looking for where the graph is below the x-axis; that is, where the polynomial is less than zero. And since this is an "or equal to" inequality, I'll be including the interval endpoints (that is, the zeroes) in my solution. (I'll not be including infinity as an endpoint, though, because infinity is not a number.)
They've given me this polynomial in already-factored form, so I can skip the factorizing step and go straight to finding zeroes and intervals.
There is a zero at x = 5, and this zero occurs twice (that is, it is a repeated zero) because the factor generating the zero occurs twice.
The other two factors generate zeroes at x = 1 and at x = −3, so my intervals are at:
(−∞, −3), (−3, 1), (1, 5), (5, +∞)
If I went to the trouble of multiplying the factors together, I'd get a positive quartic (that is, a right-side up degree-4) polynomial whose graph crosses the x-axis at x = −3 and x = 1, but it only touches the x-axis (and then turns back the way it came) at x = 5. So the graph would look something like this:

(The "graph" above is a complete kludge, and is meant only for keeping track of the general behavior of the polynomial. This is *not* an accurate graph.)
So my solution will include the one interval where the polynomial is below the axis, (−3, 1), along with that interval's endpoints. In addition, I'll also have the one other point (x = 5) where the polynomial is equal to zero. But suppose I weren't so familiar with the polynomial's shape and behavior. I could still find the answer with a factor table.
I'll make a table of the intervals and the factors:
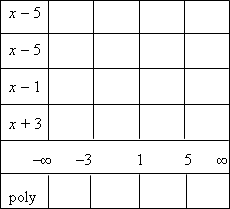
To fill the table's rows, I'll solve each factor for where it's positive:
x − 5 > 0 ⇒ x > 5
x − 1 > 0 ⇒ x > 1
x + 3 > 0 ⇒ x > −3
Now I can insert the factors' signs on the various intervals:
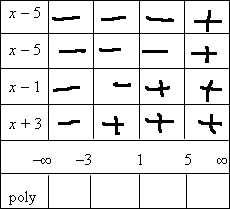
I can now multiply the signs on each interval (that is, down each column) to find the sign of the polynomial on that interval:
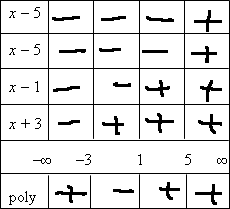
Checking the original exercise, I see that I am looking for the intervals where the polynomial is below the x-axis. Clearly, the interval [−3, 1] is in the solution. But the "or equal to" part of this inequality means that I need to take a careful look at the last two intervals on the number line.
Advertisement
The last two intervals both show "plus" signs; the polynomial is above the axis on these intervals. But what about the interval endpoint between these two intervals? What about the endpoint x = 5?
Because the factor x − 5 occurs an even number of times (in this case, it occurs twice), then the graph just touches the axis, before turning around and heading back up and away from the axis. This "just touches" point is where the polynomial equals zero. And I have to include the "equals" part in my solution, too.
Therefore, the solution, including the "or equal to" part, is:
[−3, 1], {5}
Notice the formatting of the one solution "interval" that actually contains only the one point; namely, the point x = 5. This is called a "singleton" set, because it contains only one point. For singleton sets, use curly braces, as I did above, to indicate that the set contains just the one point, or else use inequality notation (if you're allowed) to write the solution as:
−3 ≤ x ≤ 1 and x = 5
Always be careful with "or equal to" inequalities, and remember to check the endpoints; you may have a singleton set that is part of the solution, or you might find that two intervals should actually be joined into one larger interval by a shared endpoint.
Content Continues Below
- Find the solution: (x2 + 2)(x + 5)3(4 − 2x)(x2)(x − 6) ≤ 0
Thank goodness, this is already factored for me, so I can get straight to splitting the number line with the zeroes. (If they hadn't factored this already, I'd have had to start by solving a degree-9 equation!)
The zeroes are at:
x = −5, 2, 0, 6
But to find the signs on the factors, I'll need to be a little more thorough, because I've got a backwards factor (being the 4 − 2x) and a zero-free factor (being the unfactorable quadratic x2 + 2).
x2 + 2 ≥ 0 ⇒ x2 ≥ −2 is true for all x
x + 5 ≥ 0 ⇒ x ≥ −5 (three times)
4 − 2x = −2(x − 2) (two factors):
−2 ≥ 0 is never true
x − 2 ≥ 0 ⇒ x ≥ 2
x2 ≥ 0 ⇒ x ≥ 0 (twice)
x − 6 ≥ 0 ⇒ x ≥ 6
Here's my factor table with the signs inserted:

(Note the doubled and tripled factors, corresponding to the powers on those factors. Don't forget to take factors' multiplicities into account.)
Affiliate
Checking back with the original exercise, I see that they're wanting the intervals where the polynomial is negative. Then the solution intervals are (−5, 0), (0, 2), and (6, +∞).
But this is an "or equal to" inequality, so I also have to include the endpoints. That is, the points −5, 0, 2, and 6 are also part of the solution.
By adding 0 to the solution, I will join together the two intervals (−5, 0) and (0, 2) into one interval , turning "[−5, 0] and [0, 2]" into "[−5, 2]".
Then my whole solution is:
[−5, 2], [6, +∞)
Technical note: "Infinity" is not a number, so it can never be included as an interval endpoint. Never draw a square bracket at "infinity".
Practical note: This last example shows why, and where, the factor-table method is most helpful. Can you imagine trying to picture this polynomial in your head?
URL: https://www.purplemath.com/modules/ineqpoly2.htm
You can use the Mathway widget below to practice solving polynomial inequalities. Try the entered exercise, or type in your own exercise. Then click the button and select "Solve the Inequality for x" to compare your answer to Mathway's.
Please accept "preferences" cookies in order to enable this widget.
(Click "Tap to view steps" to be taken directly to the Mathway site for a paid upgrade.)
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()




