How Can 0.999… be equal to 1?

But then, one-third is a fraction, and we're used to fractions being equal to non-terminating (that is, infinite) decimal expansions. So maybe it's easier for us to accept the equality when we're dealing with thirds? (I'm guessing, but psychology may play some part in this.)

Maybe it's just that it feels wrong that something as nice and neat and well-behaved as the number 1, "the unit", the basis of so much of our arithmetical and mathematical understanding, could also be written in such a messy form as 0.9999…. Whatever the reason, many students (me included) have, at one time or another, felt uncomfortable with this equality.

What is 0.999… equal to?

The infinite repeating decimal 0.999… is equal to the whole number 1. This is very different from the value of, say, 0.999, which is equal to (which is close to 1, but not equal to 1). The ellipsis (ell-IPP-siss) — that is, the "dot, dot, dot" — after the last 9 in 0.999… makes all the difference.

What's the difference between 0.999 and 0.999…?

When I say "0.9999…", I don't mean 0.9 or 0.99 or 0.9999 or 0.999 followed by some large but finite (that is, some large but limited) number of 9's. The ellipsis (that is, the "dot, dot, dot") after the last 9 in 0.999… means "this goes on forever in the same manner".

In other words, the dot, dot, dot says that 0.9999… never ends. There will always be another 9 to tack onto the end of 0.9999…, no matter how many 9s you already have. So don't object to 0.9999… = 1 on the basis of "however far you go out, you still won't be equal to 1", because there is no "however far" to go out to; you can always go further. There is no end to an infinite decimal expansion; there will always be more 9s.

"But", some say, "there will always be a difference between 0.9999… and 1." Well, sort of. Yes, at any given stop, at any given stage of the expansion, for any given finite number of 9s, there will be a difference between 0.999…9 and 1. That is, if you do the subtraction, 1 − 0.999…9 will not equal zero.

But the point of the "dot, dot, dot" is that there is no end to the 9s; 0.9999… is inifinte. There is no "last" digit. So the "there's always a difference" argument betrays a lack of understanding of the infinite. (That's not a criticism, per se; infinity is a messy topic, and you haven't yet been given the tools with which to try to understand it.)

What about the 1 at the end of the subtraction?

When you subtract a number from itself, the result is zero. For instance, 4 − 4 = 0. So what is the result when you subtract 0.999… from 1? For shorter subtractions (that is, for the subtractions that involve only a finite number of 9s), you get:

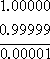
Then what about 1.000... − 0.999…?

As you can see above, for every 9 that is tacked on to the end of the decimal expansion, the subtraction of the result from 1 gives you 0.0…01, another zero is added between the decimal point and the 1 at the end. If you tacked on a hundred more 9s, the result of the subtraction from 1 would have a hundred more zeroes before the final 1.

Thus, logically, if you are working with 0.999… (that is, the expansion with infinitely-many 9s), then, after subtraction, you'll get an infinite string of zeroes. "But," you ask, "what about that '1' at the end?" Ah, but 0.999… is an infinite decimal; there is no "end", and thus there is no "1 at the end". The zeroes go on forever. And 0.000... = 0.

This says that 1 − 0.999… = 0.000... = 0, and therefore that 1 = 0.999….

But aren't they really two different numbers?

If two numbers are different, then you can fit another number between them, such as their average. But what number could you possibly fit between 0.999… and 1.000...?

How do you prove 0.999… equals 1?

You can prove that 0.999… = 1 by various methods, such as:

• using an infinite series
• multiplying by 3
• doing some algebraic manipulation

Let's investigate each of these options.

How can an infinite series prove that 0.999… = 1?

The number 0.999… can be expanded and then converted into an infinite geometric series.

Recall that, if the common ratio r of a geometric series is less than 1 (in absolute value), then there is a formula for finding the infinite expansion's "closed form" (that is, for finding the formula that can convert the expansion into a fraction of some form).

The number 0.9999… can be expanded as:

In other words, each term in this endless summation will have a 9 preceded by some number of zeroes. This may also be written in fractional form as:

That is, 0.999… is an infinite geometric series with first term and common ratio . Since the size | r | of the common ratio is less than 1, we can use the infinite-sum formula to find the value of the summation of these infinitely-many fractions:

In this way, the infinite-series summation formula proves that 0.9999… = 1.

---

How does prove that 0.999… = 1?

If you haven't already learned that in decimal form, you can prove this easily by doing the long division:

...and so on and so forth, ad infinitum.

Obviously, . Reasonably then, 0.333… + 0.333… + 0.333… = 3(0.333…) should also equal 1. But 3(0.333…) = 0.999…. Therefore, 0.999… must be equal to 1.

How can algebra prove that 0.999… = 1?

The expression 0.999… is some number; it has some value, and we'll call this numerical value x, so 0.999… = x. Now multiply this equation by ten:

Subtract the first equation from the second equation:

Dividing through by 9 to solve for the value of x, we find that x = 1. This then means that 0.999… = 1.

"But," you ask, "when you multiply by ten, that puts a zero at the end, doesn't it?" For finite expansions, certainly; but 0.999… is infinite. There is no "end" after which to put that alleged zero.

But won't 0.999… always be a little bit smaller than 1?

A common objection to 0.999… equalling 1 is that, while 0.999… may "get arbitrarily close to" 1, it is never actually equal to 1. But what is meant by the phrase "gets arbitrarily close to"? It's not like the number is moving at all; it is what it is, and it just sits there, blinking at you. It doesn't come or go; it doesn't move or get close to anything.

On the other hand, the terms of the associated sequence, 0.9, 0.99, 0.999, 0.9999, …, etc, do get arbitrarily close to 1, in the sense that, for each term in the progression, the difference between that term and 1 gets smaller and smaller as the number of 9s gets bigger. No matter how small you want that difference to be, I can find a term where the difference is even smaller.

This "getting arbitrarily close" process refers to something called "limits". You'll learn about limits later, probably in calculus. And, according to limit theory, when the value of one thing can "get arbitrarily close" to the value of another thing, this means that the two things are equal; in this case, it means that 0.999… does indeed equal 1.