Print-friendly page

Graphing Exponential Functions: Intro (page 1 of 4)

Sections: Introductory concepts, Step-by-step graphing instructions, Worked examples

Graphing exponential functions is similar to the graphing you have done before. However, by their nature, the points in an exponential function tend either to be very close to one fixed value or else to be too large to be conveniently graphed. So there will generally be only a few points that are reasonable to plot for drawing your picture, which will require that you have a good grasp of the general behavior of an exponential, so you can "fill in the gaps", so to speak.

Remember that the basic property of exponentials is that they change by a given proportion over a set period of time. For instance, a medical isotope that decays to half the previous amount every twenty minutes and a bacteria culture that triples every day each exhibit exponential behavior, because, in a given set amount of time (twenty minutes and one day, respectively), the quantity has changed by a constant proportion (one-half as much or three times as much, respectively).

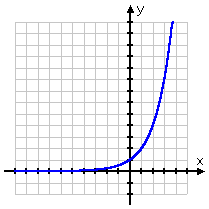
On the left-hand side of the x-axis, the graph appears to be on the x-axis. But the x-axis represents y = 0, and can you ever turn "2" into "0" by raising it to a power? Of course not. And a positive "2" cannot turn into a negative number by raising it to a power, so the line never goes below the x-axis into negative y-values, either. So, appearances to the contrary, the graph of y = 2^x is always actually above the x-axis.

So why does it look like it is right on the axis? Well, remember what negative exponents do: they say to flip the base to the other side of the fraction line. So if x = –4, we would get 2^–4, which is 2⁴ = 16, but flipped underneath to be ¹/₁₆, which is fairly small. And, by nature of exponentials, every time we go back (to the left) by 1 on the x-axis, the line is only half as high above the x-axis. That is, while y = ¹/₁₆ for x = –4, the line will be only half as high, at y = ¹/₃₂, for x = –5. So, while the line never actually touches or crosses the x-axis, it sure gets darned close! Which is why, practically speaking, the left-hand side of a basic exponential tends to be drawn right along the axis. If you zoom in close enough on the graph, you will be able to see that the graph is really above the x-axis, but it's close enough to make no difference, at least as far as graphing is concerned.

But you should not forget that this is just a mark of the limitations of the technology. Like I frequently tell my students: "Student smart; calculator stupid". You need to remember that, no matter what the calculator says, the graph is still above the x-axis; the y-values are still positive, though very, very, very small.   Copyright © Elizabeth Stapel 2006-2008 All Rights Reserved

You can see that, on the right-hand side of the x-axis, the graph shoots up through the roof. This is again because of the doubling behavior of the exponential. Once the functions starts visibly growing, it keeps on doubling, so it gets very large, very fast.

You will not generally be plotting many points on the left-hand side of the graph, because the y-values get so close to zero as to make the plot-points indistinguishable from the x-axis. And you will not generally be plotting many point on the right-hand side of the graph, because the y-values get way too big. This is why I've gone on at length (above) about the general shape and behavior of an exponential: You will need this knowledge to help you with the graphing, so make sure you have a fairly good grasp of it.

Top  |  1 | 2 | 3 | 4  |  Return to Index  Next >>

  Copyright © 2006-2008  Elizabeth Stapel   |   About   |   Terms of Use

 Feedback   |   Error?