Return to the Purplemath home page

 

Return to the Lessons Index  | Do the Lessons in Order  |  Print-friendly page

Determinants: 2×2 Determinants (page 1 of 2)

Sections: 2×2 determinants, 3×3 determinants

Determinants are like matrices, but done up in absolute-value bars instead of square brackets. There is a lot that you can do with (and learn from) determinants, but you'll need to wait for an advanced course to learn about them. In this lesson, I'll just show you how to compute 2×2 and 3×3 determinants. (It is possible to compute larger determinants, but the process is much more complicated.)

If you have a square matrix, its determinant is written by taking the same grid of numbers and putting them inside absolute-value bars instead of square brackets:

    If this is "the matrix A" (or "A")...

    ...then this is "the determinant
    of     A" (or "det A").

      
    [[ 1 0 3 ][ 6 -2 1 ][ 0 3 0 ]]
      

      
    || 1 0 3 || 6 -2 1 || 0 3 0 ||
      

Just as absolute values can be evaluated and simplified to get a single number, so can determinants. The process for evaluating determinants is pretty messy, so let's start simple, with the 2×2 case.

For a 2×2 matrix, its determinant is found by subtracting the products of its diagonals, which is a fancy way of saying in words what the following says in pictures:

the matrix A

the determinant of A ("det A")

[[ a b ][ c d ]]

animation: det(A) = ab - cb

the matrix A

the determinant of A ("det A")

[[ 1 2 ][ 3 4 ]]

animation: det(A) = (1)(4) - (3)(2) = 4 - 6 = -2

In other words, to take the determinant of a 2×2 matrix, you multiply the top-left-to-bottom-right diagonal, and from this you subtract the product of bottom-left-to-top-right diagonal.

"But wait!" I hear you cry; "Aren't absolute values always supposed to be positive? You show that second matrix above as having a negative determinant. What's up with that?" You make a good point. Determinants are similar to absolute values, and use the same notation, but they are not identical, and one of the differences is that determinants can indeed be negative.

  • Evaluate the following determinant:

      • || 1 -4 || 0 3 ||

    I multiply the diagonals, and subtract:   Copyright © Elizabeth Stapel 2004-2011 All Rights Reserved

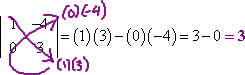
      (1)(3) - (0)(-4) = 3 - 0 = 3

  • Find the determinant of the following matrix:

      • [[ 2 1 ][ -1 3 ]]

    I convert from a matrix to a determinant, multiply along the diagonals, subtract, and simplify:

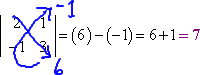
      (6) - (-1) = 6 + 1 = 7

 Top  |  1 | 2  |  Return to Index  Next >>

Cite this article as:

Stapel, Elizabeth. "Determinants: 2x2 Determinants." Purplemath. Available from
    https://www.purplemath.com/modules/determs.htm. Accessed
 

 

Purplemath:
  Linking to this site
  Printing pages
  School licensing

Reviews of
Internet Sites:
   Free Help
   Practice
   Et Cetera

The "Homework
   Guidelines"

Study Skills Survey

Tutoring from Purplemath
Find a local math tutor

  Copyright © 2004-2012  Elizabeth Stapel   |   About   |   Terms of Use

 

Contact Us