Regarding Horizontal and Slant Asymptotes
Purplemath
All of the horizontal and slant asymptote rules can be viewed as pretty much reducing to doing the same thing: dividing the numerator polynomial by the denominator polynomial, and ignoring the fractional part.
How so? Let's examine this.
Content Continues Below
When the degree is greater in the denominator, then the polynomial fraction is like a proper fraction (such as ) which cannot be converted to a mixed number other than trivially (as "").
For instance, given the following rational function:
...you can't do any long division, because the denominator is of higher degree than is the numerator. The best you can do is to restate the function as:
So, ignoring the fractional portion, you know that the horizontal asymptote is y = 0 (the x-axis), as you can see in the graph below:
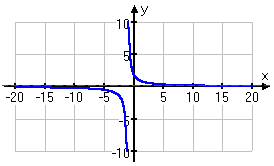
If the degrees of the numerator and the denominator are the same, then the only division you can do is of the leading terms.
For instance, given the following function:
...you can only do one trivial step in the division:
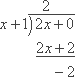
...which means that the original function converts to mixed-number form fairly trivially as:
So, ignoring the fractional part, you know that the horizontal asymptote is y = 2, as you can see in the graph below:
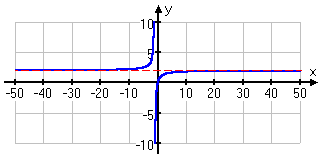
Content Continues Below
If the degree is higher on top, then the division gives a polynomial whose degree is the difference between the degrees of the numerator and denominator. Since you'll almost certainly only be doing rationals where the numerator's degree is at most 1 greater than the denominator's degree, then the division will only give you, at most, a linear (straight-line) expression.
For instance, given the following rational function:
...you do the long division:
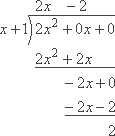
...and get:
So, ignoring the fractional part, you know that the slant asymptote is y = 2x − 2, as you can see in the graph below:
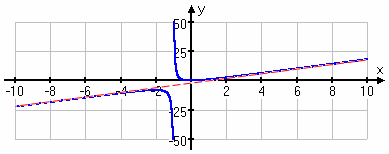
In a sense, then, you're always using long division to find the horizontal or slant asymptote. It's just that the long division is explicitly necessary only for finding the slant asymptote.
URL: https://www.purplemath.com/modules/asymnote.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()



