Special Angle Values: How to Remember Them
Purplemath
There are a few (a very few) angles that have relatively "neat" trigonometric values, involving, at worst, one square root. Because of their relatively simple values, these are the angles which will typically be used in math problems (in calculus, especially), and you will be expected to have these angles' values memorized.
You will be expected to use these values to provide "exact" answers for solving right triangles and for finding the values of various trigonometric ratios.
Usually, textbooks present these values in a table that you are expected memorize. But pictures are often easier to recall on tests, etc, at least for some of us. If those tables aren't working for you, then this lesson will show the way in which many people (including me!) really keep track of these values.
Content Continues Below
In what follows, I use degrees for the angle measures. This is usually how students are introduced to angle measures. However, in case you're working with radians, I'll also note the radian angle-measure equivalents.
45°-Angle Values (from a 45-45-90 triangle)
All 45-45-90 triangles are similar; that is, they all have their corresponding sides in ratio. (An angle measuring 45° is, in radians, .) So let's look at a very simple 45-45-90:
![45° triangle, with sides having lengths sqrt[2] and hypotenuse having length 2; the right angle is at the right of the base; the base angle is at the left of the base; the opposing angle is to the upper right](trig/trig05.gif)
The hypotenuse of this triangle, shown above as 2, is found by applying the Pythagorean Theorem to the right triangle with sides having length . The base angle, at the lower left, is indicated by the "theta" symbol (θ, THAY-tuh), and is equal to 45°. So how does knowing this triangle help us?
It helps us because all 45-45-90 triangles are similar. Therefore, every "evaluation" or "solve the triangle" question involving a 45-45-90 triangle or just a 45° angle can be completed by using this triangle. This picture is all you'll need.
30°- and 60°-Angle Values (from a 30-60-90 triangle)
When we need to work with a 30- or a 60-degree angle, the process is similar to the above, but the set-up is a bit longer. (A 30° angle is equivalent to an angle of radians; a 60° angle is equivalent to an angle of radians.)
For either of the angles, this is the triangle that we start with:
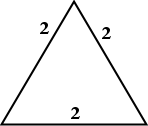
This is a 60-60-60 triangle (that is, an equilateral triangle), with sides having a length of two units.
We drop the vertical bisector from the top angle down to the bottom side:
![equilateral triangle split in half by dropping a vertical line from the peak angle down to the middle of the base; each new peak angle is labelled as beta, and each base angle is labelled as alpha; the two halves of the original base are labelled 1; the altitude is labelled sqrt[3]; and the sides (now hypotenuses) are still labelled 2](trig/trig02.gif)
Note that this bisector is also the altitude (height) of the triangle.
Affiliate
By using the Pythagorean Theorem, we get that the length of the bisector is . And this bisector has formed two 30-60-90 triangles.
Advertisement
When we are working with a 60-degree angle, we use the left-hand triangle above, at it stands, with the base angle (at the left) labelled "α" (AL-phuh, being the funny-looking "a"):
![60° triangle, with alpha at the lower left-hand corner, the base (the adjacent side) having length 1, the altitude (the opposite side, on the right) having length sqrt[3], and the hypotenuse having length 2](trig/trig03.gif)
When we are working with a 30-degree angle, we use the right-hand triangle, knocked over to the left, base angle (at the left) labelled "β" (BAY-tuh, being the funny-looking "b"):
![30° triangle, with beta in the lower left-hand corner, the base (the adjacent side) having length sqrt[3], the altitude (the opposide side, on the right) having length 1, and the hypotenuse having length 2](trig/trig04.gif)
We can find trigonometric values and ratios with the 30-degree and 60-degree triangles in the exact same manner as with the 45-degree triangle. The above pictures are all you'll need.
You may get one of those teachers who doesn't want you to draw these pictures (because you're supposed to have everything memorized by now). Well, this is why your pencil has an eraser. My Calculus II instructor said that if we drew the pictures on our tests, the entire problem would be counted wrong. I drew the pictures anyway, but very lightly, and erased them all before I handed the tests in. He never knew, and I passed the course. You do what you gotta do.
Content Continues Below
Using a Table
The pictures above are what I've always used, and many find them helpful. On the other hand, some people prefer tables or other methods. If tables work better for you, then this table comes highly recommended, having been "field-tested" by a working instructor:
|
|
30° |
45° |
60° |
sin |
1 |
2 |
3 |
|
cos |
3 |
2 |
1 |
|
|
|
divided by 2 |
||
To find, say, the sine of an angle measuring forty-five degrees, you would trace across in the "sin" row and down the "45°" column, taking the square-root symbol with you as you go and remembering to include the "divided by 2" from the bottom, to get . The neat pattern of "1, 2, 3" across the top row and "3, 2, 1" across the middle row are meant to help you memorize the table values. Keep in mind that the square root of 1 is just 1, so, for instance, . To find the tangent, you'd divide the sine value by the cosine value.
Using Your Fingers
Another method uses your left hand to essentially do the same thing. With your palm facing you, count off the basic reference angles, starting with your thumb: 0°, 30°, 45°, 60°, and 90°.
Affiliate
To find a trig value, you'll lower the finger corresponding to that angle, keeping your palm facing you. For the sine value, you'll take the square root of the number of fingers to the left of the lowered finger, and divide by 2; for the cosine value, you'll take the square root of the number of fingers to the right of the lowered finger, and divide by 2; for the tangent, you'll divide the square root of the number of fingers to the left by the square root of the number to the right (and rationalize, as necessary).
For instance, if you're wanting to work with a thirty-degree angle, you'd orient your hand like this:

The sine is the square root of your thumb (that is, the square root of "one") over two, which yields:
The cosine is the square root of your three fingers (that is, the square root of "three") over two, yielding:
On the other hand, if you're wanting to evaluate sin(0°), cos(0°), and cot(0°), you'd orient your left hand like this:

Since your thumb is folded down, there are 0 fingers to the left, and 4 fingers to the right. Then the values of the sine and the cosine are found as:
The cotangent is the reciprocal of the tangent. What is the value of the tangent?
Flipping the above would cause division by zero, which isn't allowed. So cot(0°) is undefined.
(An angle measuring 0° is equivalent to an angle of 0 radians. An angle measuring 90° is equivalent to an angle of radians.)
URL: https://www.purplemath.com/modules/specang.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()