Factoring Polynomials
Purplemath
As pointed out on the previous page, synthetic division can be used to check if a given x-value is a zero of a polynomial function (by returning a zero remainder) and it can also be used to divide out a linear factor from that polynomial (leaving one with a smaller-degree polynomial).
Because of this close relationship between zeroes (of polynomial functions) and solutions (of polynomial equations), the techniques used for "solving" polynomials can be applied equally well to finding the complete factorization of a polynomial.
Content Continues Below
Advertisement
The major difference between the "solving" exercises on the previous page and the "factoring" exercises on this page is that, for factoring, we have to keep track of any numbers that we divide off. An example of this would be the 2 that I divided out of the quadratic near the end of the example on the previous page. When solving "(polynomial) equals zero", we don't care if, at some stage, the equation was actually "2×(polynomial) equals zero". But, for factoring, we care about that initial 2.
Also, when we're doing factoring exercises, we may need to use the difference- or sum-of-cubes formulas for some exercises. This is less common when solving.
On the "plus" side, though, the polynomials for "factoring" exercises generally involve nicer numbers, without the complex-number values or the messy square roots common in "solving" exercises.
-
Completely factor: 30x5 − 166x4 − 542x3 + 2838x2 + 1520x − 800
All the coefficients are even, so I can factor a 2 out front. But this isn't an "equals zero" equation, so I can't just "divide off" the 2, making it disappear. Instead, I'm going to have to remember to include that factor of 2 in my final factored form.
At this point, I have the following:
2(15x5 − 83x4 − 271x3 + 1419x2 + 760x − 400)
Even after putting aside the 2, I'm still stuck with some pretty big numbers:
15x5 − 83x4 − 271x3 + 1419x2 + 760x − 400
Affiliate
The Rational Roots Test would give me a staggeringly-long list of possible roots, including loads of fractions. At least at first, I'm going to just stick with whole-number factors of 400. I'll figure out the whole long list later — if I have to.
Since the solutions to polynomials are usually pretty "close to the middle", I won't bother testing solutions like x = 400 in my synthetic division, at least not initially. Instead, I'll keep my first guesses small.
Before I start guessing, though, I'll check the graph:
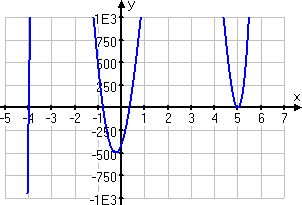
It looks like −4 and 5 would be excellent first choices to plug into my synthetic division. The graph at x = 5 bounces off the axis, so I'm guessing that this is a repeated root. I'll try the synthetic division first, and I'll try it twice:
![synthetic division with x = 5 outside on the left; the first row inside the first division is 15 −83 −271 1419 760 −400; the second row is [empty space] 75 −40 −1555 −680 400; the answer row is 15 −8 −311 −136 80 0; the previous row is the first inside row for the second division with x = 5; the second row inside is [empty space] 75 335 120 −80; the new answer row is 15 67 24 −16 0](polysolv/solve10.gif)
So I've pulled out two copies of the factor x − 5. I know the factors I've taken out; the last line of the synthetic division above tells me that my polynomial is now:
2 (x − 5)2 (15x3 + 67x2 + 24x − 16)
The part of the expression that I have left to factor is the cubic in the last parentheses above. (How did I know it was a cubic? Because they gave me something of degree-five, and I've taken out two linear factors.)
To check my work (and to confirm the identity of the last "nice" zero), I'll graph the polynomial function related to that remaining cubic factor, being the 15x3 + 67x2 + 24x − 16:

So it looks like x = −4 is still a value that I want to check. Here's my synthetic division:
![synthetic division with x = −4; the second row is [space] −60 −28 16; and the final row is 15 7 −4 0](polysolv/solve12.gif)
I was right; x = −4 is a zero. Taking out the x + 4 factor leaves me with just a quadratic factor left:
15x2 + 7x − 4
I can use regular factoring methods to finish the factorizing:
15x2 + 7x − 4 = (5x + 4)(3x − 1)
(By the way, these two factors created the two "messy" roots on the graph, being and .)
Now I need to go back through my work, and collect all of my factors, starting with the initial 2 that I factored out. My complete factorization is:
2(x − 5)2(x + 4)(5x + 4)(3x − 1)
In your hand-in answer, the factors with variables don't have to be listed in any particular order, since order doesn't matter for multiplication. But any constant term, such as the "2", should go in front. And many books prefer repeated factors to be written in exponential form, like the "(x − 5)2" in my final answer above.
Content Continues Below
By the way, if you don't have a graphing calculator, you've got a rough road ahead of you. For answering these factoring questions, you'll want to start with the Rational Roots Test. Working from the list provided by the Test, you'll want to start testing the smaller whole-number values, usually being factors of the constant term, and work out from there.
Keep in mind that a "solution" of "x = a" means you have a factor of "x − a". Take any factors out that you can, and always continue you work with whatever is the smaller, simpler polynomial that remains. And do a quick check, at least of the new constant term, to see if there are Test values that you can eliminate as you go.
Affiliate
In lieu of graphing, there is trick you can use with the synethetic division for knowing when to stop moving to higher or lower Test values. Also, you may find Descartes' Rule of Signs to be helpful, as it can tell you about the maximum numbers of positive or negative zeroes that the polynomial could have.
I would also suggest doing as many practice problems as you can, because your having given that particular mental muscle a solid work-out could make a big difference on the next test.
-
Factor fully: 3x6 − 12x5 + 12x4 + 24x3 − 96x2 + 96x
Not only can I pull a 3 out front, but I can also pull out an x. Doing so leaves me to factor:
x5 − 4x4 + 4x3 + 8x2 − 32x + 32
The possible zeroes of the quintic (that is, the degree-five) polynomial will be plus and minus the factors of thirty-two, or:
±1, 2, 4, 8, 16, 32
I can try the trick with simply plugging in x = −1:
−1 − 4 − 4 + 8 + 32 + 32 = 63
Not even close. What about x = 1?
1 − 4 + 4 + 8 − 32 + 32 = 9
Okay; I guess I'll try the next biggest possibilities. How about x = 2?
![synthetic division with 2 outside on the left; the first row inside is 1 −4 4 8 −32 32; the second row inside is [empty space] 2 −4 0 16 −32; the answer row is 1 −2 0 8 −16 0](polysolv/solve18.gif)
Finally! The last row above tells me that x = 2 is a zero, so (x = 2) is a factor. Removing that factor, I'm left with the following:
x4 − 2x3 + 8x − 16
The above terms can be paired, I notice, in such as way that I can factor this directly:
(x4 − 2x3) + (8x − 16)
x3(x − 2) + 8(x − 2)
(x − 2)(x3 + 8)
Obviously, x − 2 is another factor. So now I'm left with the cubic. And this is a sum of cubes, so I'll use that formula to complete the factorization:
(x + 2)(x2 − 2x + 4)
(I remember, from back when I learned about sums and differences of cubes, that the quadratic factor doesn't factor. So I know I'm done at this point.)
Now I got back to the beginning, and make sure I snag all of the factors I pulled out along the way. My final answer, which is:
3x(x − 2)2(x + 2)(x2 − 2x + 4)
URL: https://www.purplemath.com/modules/solvpoly2.htm
Select a Course Below
Standardized Test Prep
Homeschool Math
© 2024 Purplemath, Inc. All right reserved. Web Design by ![]()




