Examples of the Method of Common Differences
Purplemath
Whenever you've been given a listing of integers (that is, whole numbers and maybe some of their negatives), and you can't see any obvious pattern in the list of numbers, you can always try the method of common differences to try to find a polynomial rule for the list's terms.
Note: There can be *many* different rules that will generate a given sequence of numbers. But the method of common differences will *always* give you a polynomial rule in the end.
- Find the next number in the following sequence: 0, 12, 10, 0, −12, −20,....
Uh.... I could try to cast about for a formula for this sequence, but I think I'll go right to finding differences by subtracting each term from its following term:
The first row above is the sequence they gave me; the second row above is the first differences (which didn't match); the third row above is the second differences (which also didn't match); and the fourth row above is the third differences (which finally matched).
Since the third differences are all the same (in this case, "6"), this tells me tht the generating polynomial for this sequence is a cubic, or third degree, polynomial, so it is of the form:
an3 + bn2 + cn + d
I'll evaluate this at some of the (smaller) values of n:
a(1)3 + b(1)2 + c(1) + d
= a + b + c + d = 0
a(2)3 + b(2)2 + c(2) + d
= 8a + 4b + 2c + d = 12
a(3)3 + b(3)2 + c(3) + d
= 27a + 9b + 3c + d = 10
a(4)3 + b(4)2 + c(4) + d
= 64a + 16b + 4c + d = 0
This gives me four equations in four unknowns. I'll use matrices again to solve:
Then a = 1, b = −13, c = 44, and d = −32, so the formula is:
1n3 + (−13)n2 + 44n + (−32)
= n3 − 13n2 + 44n − 32
They gave me the first six terms of the sequence, so I need to give the seventh term, which is:
(7)3 − 13(7)2 + 44(7) − 32
= 343 − 637 + 308 − 32
= −18
Sometimes the common differences don't work out (that is to say, you don't end up with a row of all equal numbers), but the table of differences still contains useful information.
- Find the next term in the following sequence: 2, 4, 8, 16, 32,....
You might notice right away that every term is gotten by multiplying the previous term by 2. That is, the formula in this case is not a polynomial, but an exponential: an = 2n In math-speak, the n-th term an ("ay-sub-enn") is 2 to the power n. But what if you didn't happen to notice this? What would happen if you tried to find the differences?
I will try to find the common difference:
As you can see, I am not arriving at a common difference. However, do you see something interesting in the diagonal rows? In each top-left-to-bottom-right diagonal, the values are the same! For sequences where the rule is "multiply by some fixed amount", the diagonals are always multiplied by one less than this fixed amount. Since the rule for this sequence is "multiply by 2", the entries on the diagonals are multiplied by 1, which is why they are unchanged going down the diagonals.
In either case, I came up with the rule "multiply the last term by 2 to get the next term", so the next term here is:
2(32) = 64
Note, however, that the above is not the only valid answer. I could have continued with the subtractions, with the last row being just "2". This is just one number, but, in accordance with the rules for common differences, there are no other numbers in that row that don't equal 2, so I can treat this like it's telling me that a fourth-power polynomial will fit the points they gave me.
Using the index (that is, the n-value) for the input and the sequence values as the outputs, I get this system of equations:
a + b + c + d + e = 2
16a + 8b + 4c + 2d + e = 4
81a + 27b + 9c + 3d + e = 8
256a + 64b + 16c + 4d + e = 16
625a + 125b + 25c + 5d + e = 32
Plugging this into my graphing calculator, I get the following solution polynomial:
While this modelling polynomial is much more painful than was the exponential solution, it is still a valid formula for the sequence. The answer given by finding a polynomial from the common differences might be messy, but common differences will always give you an answer.
- Find the next term in the following sequence: 1, −3, 9, −27, 81,....
In this case I am almost multiplying by 3, but "multiply by 3" doesn't account for the minus sign. Notice, though, that the minus sign alternates; only every other term is negative. This means that we are multiplying by a negative three, so the next term is:
−3(81) = −243
By the way, the differences in this case look like this:
Going down each diagonal (highlighted in color, above), you can find the multiplier for each row by taking the lower number and dividing by the higher number. For instance, 12 ÷ −3 = −4 and 144 ÷ −36 = −4. Since the multiplier for the table of differences is one less than the multiplier for the sequence, then the sequence multiplier is one more than the table multiplier, or −4 + 1 = −3, which we already knew.
- Find the next term in the following sequence: 5, 7, 9, 11, 13,...
These numbers aren't growing really quickly, so this doesn't appear to be a "multiply by some fixed value" kind of sequence. Supposing I didn't notice right away that the rule is "add two to the previous value", I can still find the answer from the table of differences:
Since the first differences are the same, this means that the rule is a linear polynomial, something of the form y = an + b. I will plug in the first couple of values from the sequence, and solve for the coefficients of the polynomial:
1a + b = 5
2a + b = 7
This system solves as:
So the formula is y = 2n + 3. Since they gave me the first five terms, the next term will be the sixth term:
2(6) + 3 = 12 + 3 = 15
- Find the next term in the following sequence: 1, 4, 8, 13, 19, 26,...
This doesn't appear to be a "multiply by a fixed value" kind of sequence, and there doesn't appear to be a fixed value that is added each time, either. (For instance, in the last sequence, we always added 2 to get the next term.) Let's see what the differences give me:
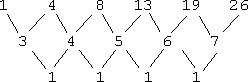
Since the second differences are the same, a formula for this sequence is a quadratic, y = an2 + bn + c. I'll plug in the first three terms for y and solve for the values of a, b, and c:
1a + 1b + c = 1
4a + 2b + c = 4
9a + 3b + c = 8
Then the formula for this sequence is . Since they gave me the first six terms, the next term will be the seventh:
Yes, sometimes you'll get a formula that contains fractions, yet spits out whole numbers. No, you'll never guess them by just looking. You'll need the method of common differences.
© 2024 Purplemath, Inc. All right reserved. Web Design by 